SICP 読書ノート#31 - 3.3.3 表の表現 (pp.156-160)
「§3.3.3 表の表現」から。
問題 3.24
解答は省略。
make-table にテスト関数を引数で渡せるようにし、
assoc-tree 内の equal? の代わりに
そのテスト関数を使えばよいだけ。
問題 3.25
テキストの例がわかりづらいのと、問題3.26でリスト構造を 単方向リストから二分木へ入替を睨んで、以下のようにモジュール分割する。
- key、valueの対で持つrecord
- recordをリスト構造で管理するtreeとその操作
- テーブル本体 (treeの操作で実装)
まずはrecord。key、valueの対である。
(define (make-record k v) (cons k v)) (define (key record) (car record)) (define (value record) (cdr record)) (define (set-key! record k) (set-car! record k)) (define (set-value! record v) (set-cdr! record v))
次にtree。recordの単方向リストである。
(define (make-tree record next) (cons record next)) (define (record tree) (car tree)) (define (next tree) (cdr tree)) (define (set-record! tree record) (set-car! tree record)) (define (set-next! tree next) (set-cdr! tree next))
ここからtreeの操作手続き。
asscoc-tree。treeからkeyに一致するsubtreeを返す。
(define (assoc-tree tree k) (cond ((null? tree) false) ((equal? k (key (record tree))) (record tree)) (else (assoc-tree k (next tree)))))
adjoin-tree!。tree、key-list、valueを引数に取り。 key数分だけの深さを持つ木を生成しtreeへ挿入する。
(define (adjoin-tree! tree key-list v) (define (make-deep-record key-list) (if (null? (cdr key-list)) (make-record (car key-list) v) (make-record (car key-list) (make-tree (make-deep-record (cdr key-list)) nil)))) (set-next! tree (make-tree (make-deep-record key-list) (next tree))))
テーブルの初期化手続き。リスト構造の実装によって処理が変わるので、 テーブルの実体とは分けておく。
(define (make-table-tree) (make-tree (make-record '*table* nil) nil))
テーブルの実装。メソッドとしてlookup、insert、printを用意。
(define (make-table) (let ((the-tree (make-table-tree))) (define (lookup key-list) (define (iter tree key-list) ; (display (format "lookup t=~A k=~A ~%" tree key-list)) (if (null? key-list) false (let ((t (assoc-tree tree (car key-list)))) (if t (if (null? (cdr key-list)) (value (record t)) (iter (value (record t)) (cdr key-list))) false)))) (iter the-tree key-list)) (define (insert! key-list v) (define (iter tree key-list) ; (display (format "insert! t=~A k=~A v=~A ~%" tree key-list v)) (if (null? key-list) false (let ((t (assoc-tree tree (car key-list)))) (if t (if (null? (cdr key-list)) (set-value! (record t) v) (iter (value (record t)) (cdr key-list))) (adjoin-tree! tree key-list v))))) (iter the-tree key-list)) (define (print) (begin (display the-tree (current-error-port)) (newline (current-error-port)))) (define (dispatch m) (cond ((eq? m 'lookup-proc) lookup) ((eq? m 'insert-proc!) insert!) ((eq? m 'print-proc) print) (else (error "dispatch -- unknown operation" m)))) dispatch)) (define (lookup-table table key) ((table 'lookup-proc) key)) (define (insert-table! table key value) ((table 'insert-proc!) key value)) (define (print-table table) ((table 'print-proc)))
テスト。
racket@> (define tbl (make-table)) racket@> (insert-table! tbl (list 1 2) "one two") racket@> (insert-table! tbl (list 1 3) "one three") racket@> (insert-table! tbl (list 2 3) "two three") racket@> (insert-table! tbl (list 1 4) "one four") racket@> (insert-table! tbl (list 2 4) "two four") racket@> (print-table tbl) ((*table*) (2 (3 . two three) (4 . two four)) (1 (2 . one two) (4 . one four) (3 . one three))) racket@> (lookup-table tbl (list 1 2)) "one two" racket@> (lookup-table tbl (list 1 1)) #f racket@> (lookup-table tbl (list 2 1)) #f racket@> (lookup-table tbl (list 2 3)) "two three"
問題 3.26
テーブルを二分木で実装せよ、という問題。
単方向リストであれ二分木であれ、リスト構造を辿って所望のレコードを取得する/挿入する という操作は同じなので、テーブルの実体を変更する必要はない。recordもそのまま。
変更が必要なのは、リスト構造および操作手続きを単方向リストから二分木に入れ替えるだけ。
まずはtreeの実装から。left、rightを追加する。
(define (make-tree record left right) (list record left right)) (define (record tree) (car tree)) (define (left tree) (cadr tree)) (define (right tree) (caddr tree)) (define (set-record! tree record) (set-car! tree record)) (define (set-left! tree left) (set-car! (cdr tree) left)) (define (set-right! tree right) (set-car! (cddr tree) right))
treeの操作手続き。テーブルの実装はそのままとしたいので、 問題 3.25 からインターフェースは変えない。
まずはassoc-tree。keyが一致するrecordを見つけるまで枝を下っていく。
(define (assoc-tree tree k) (cond ((null? tree) false) ((equal? k (key (record tree))) tree) ((< k (key (record tree))) (assoc-tree (left tree) k)) (else (assoc-tree (right tree) k))))
次にadjoin-tree。枝がnilになるところまで下って行き、新しいsubtreeを追加する。
(define (adjoin-tree! tree key-list v) (define (make-deep-tree key-list) (if (null? (cdr key-list)) (make-tree (make-record (car key-list) v) nil nil) (make-tree (make-record (car key-list) (make-deep-tree (cdr key-list))) nil nil))) (cond ((< (car key-list) (key (record tree))) (if (null? (left tree)) (set-left! tree (make-deep-tree key-list)) (adjoin-tree! (left tree) key-list v))) ((> (car key-list) (key (record tree))) (if (null? (right tree)) (set-right! tree (make-deep-tree key-list)) (adjoin-tree! (right tree) key-list v))) (else (error "adjoin-tree! -- tree key value" tree key-list v))))
テーブルの初期化手続き。先頭のrecordは便宜的に-∞としている。
(define (make-table-tree) (make-tree (make-record -inf.0 nil) nil nil))
テスト。
racket@> (define tbl (make-table)) racket@> (insert-table! tbl (list 1 2) "one two") racket@> (insert-table! tbl (list 1 3) "one three") racket@> (insert-table! tbl (list 2 3) "two three") racket@> (insert-table! tbl (list 1 4) "one four") racket@> (insert-table! tbl (list 2 4) "two four") racket@> (print-table tbl) ((-inf.0) () ((1 (2 . one two) () ((3 . one three) () ((4 . one four) () ()))) () ((2 (3 . two three) () ((4 . two four) () ())) () ()))) racket@> (lookup-table tbl (list 1 2)) "one two" racket@> (lookup-table tbl (list 1 1)) #f racket@> (lookup-table tbl (list 2 1)) #f racket@> (lookup-table tbl (list 2 3)) "two three"
問題 3.27
フィボナッチ数列にメモ化を適用した例。
(define (memoize f) (let ((table (make-table))) (lambda (x) (let ((memo-result (lookup-table table (list x)))) (display (format "memo-ret ~A -> ~A ~%" x memo-result)) (or memo-result (let ((result (f x))) (insert-table! table (list x) result) result)))))) (define memo-fib (memoize (lambda (n) (cond ((= n 0) 0) ((= n 1) 1) (else (+ (memo-fib (- n 1)) (memo-fib (- n 2))))))))
実際に動かしてみる。一度計算された結果はメモから取り出されるだけである。
racket@> (memo-fib 3) memo-ret 3 -> #f memo-ret 2 -> #f memo-ret 1 -> #f memo-ret 0 -> #f memo-ret 1 -> 1 2
計算ステップ数
オーダーは O(n)。一度計算した結果は計算されないので、単純にNに比例するはず。
環境モデル図
まずmemo-fibの定義直後にtableが生成される。

さらに(memo-fib 3)を実行後。
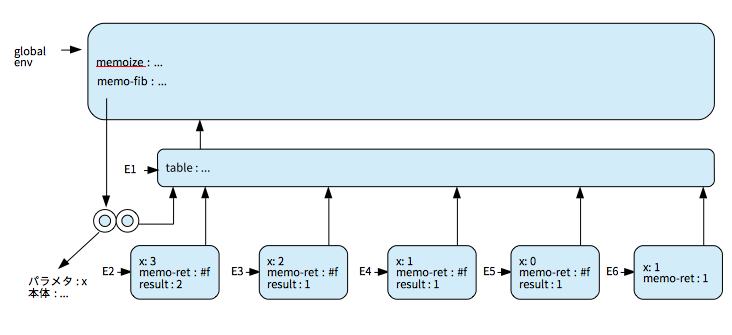
memo-fibを(memoize fib)とする
単にmemo-fib``を(memoize fib)```と定義した場合、
(define (fib n) (cond ((= n 0) 0) ((= n 1) 1) (else (+ (fib (- n 1)) (fib (- n 2)))))) (define memo-fib (memoize fib))
テスト。
racket@> (memo-fib 3) memo-ret 3 -> #f 2
fibで再帰降下してしまうので途中の計算結果がメモ化されない。
次は「§3.3.4 ディジタル回路のシミュレータ」から。