SICP 読書ノート#29 - 3.3.1 可変リスト構造 (pp.147-153)
「§3.3 可変データのモデル化」から。
可変リスト構造
構成子、選択子とは別にオブジェクトを修正する変更子(mutator)を導入する。
例えばpairの場合、
| 手続き | 呼び方 |
|---|---|
| cons | 構成子 (constructor) |
| car, cdr | 選択子 (selector) |
| set-car!, set-cdr! | 変更子 (mutator) |
ミュータブルなリストの導入
(2015/08/20追記) 実行環境がRacketの場合、Pairs and Listsはデフォルトではimmutableなので、以下のいずれかの方法でmutableなリストを導入できます。(他にもあったら教えてください)
- r5rsモジュールをロードする
- Mutable Pairs and Listsを利用する
1. R5RSモードにする
- r5rsモジュールをrequireするだけ。
requireなど一部の組み込み関数の振る舞いが変わってしまうのが、quoteもmutableになるのでこちらの方がベターかも
(require r5rs)
2. RacketのMutable Pairs and Listsを利用する
あたりを参考に、mutable-lists.scmという名前で以下のようなファイルを作る。
#lang racket ;; Datatypes - Mutable Pairs and Lists (define pair? mpair?) (define cons mcons) (define car mcar) (define cdr mcdr) (define (caar p) (mcar (mcar p))) (define (cadr p) (mcar (mcdr p))) (define (cdar p) (mcdr (mcar p))) (define (cddr p) (mcdr (mcdr p))) (define (caaar p) (mcar (mcar (mcar p)))) (define (caadr p) (mcar (mcar (mcdr p)))) (define (cadar p) (mcar (mcdr (mcar p)))) (define (caddr p) (mcar (mcdr (mcdr p)))) (define (cdaar p) (mcdr (mcar (mcar p)))) (define (cdadr p) (mcdr (mcar (mcdr p)))) (define (cddar p) (mcdr (mcdr (mcar p)))) (define (cdddr p) (mcdr (mcdr (mcdr p)))) (define set-car! set-mcar!) (define set-cdr! set-mcdr!) ;; Compatibility Collection - Mutable List Functions (require (prefix-in mlst: compatibility/mlist)) (define list? mlst:mlist?) (define list mlst:mlist) (define length mlst:mlength) (define list-ref mlst:mlist-ref) (define append mlst:mappend) (define map mlst:mmap) (define memq mlst:mmemq) (define assoc mlst:massoc) (provide (all-defined-out))
あとはこれをrequireするだけ。
(require "mutable-lists.scm")
ただし、前述のようにクォート(quote ...)に関してはmutableにできていないので一貫性にかける。
ここでは前者の方法で進めたいと思います。
後者のソースコードはGitHubにアップしているので、良かったら参考にしてみてください。
ミュータブルリストの動作
試しに動かしてみる。
racket@> (require r5rs) racket@> (define z (cons 1 2)) racket@> z (mcons 1 2) racket@> (set-car! z 3) racket@> (set-cdr! z (cons 4 5)) racket@> z (mcons 3 (mcons 4 5))
mconsという表記がうっとしい場合は、display手続きを使うとよい
racket@> (define (disp x) (display) (newline)) racket@> (disp z) (3 4 . 5)
問題 3.12
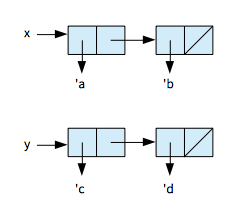
(define x (list 'a 'b)) (define y (list 'c 'd)) (define z (append x y)) (cdr x)
この段階ではxは破壊されていないので、
(cdr x) => (b)となる。
ポインタ図は以下の通り。
さらに、
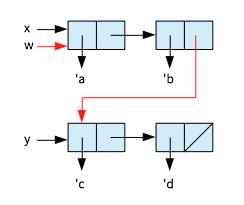
(define w (append! x y) (cdr x)
では、(append! x y)の実行時にxは破壊されているため、
(cdr x) => (b c d)となる。
ポインタ図は以下の通り。
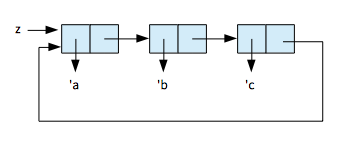
問題 3.13
循環リストが生成される。ポインタ図は以下の通り。
問題 3.14
地道にノートに書き出したら分かった。
最初は以下のようなポインタ図で、
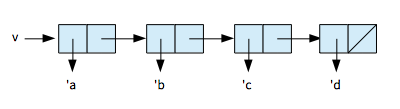
最終的には以下のようになる。
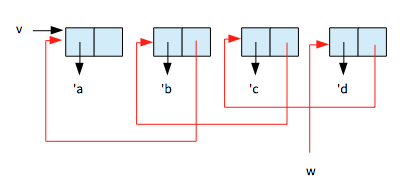
テスト。
racket@> (define v (list 'a 'b 'c 'd)) racket@> (disp v) (a b c d) racket@> (define w (mystery v)) racket@> (disp w) (d c b a) racket@> (disp v) (a)
共有と同一
eq?は参照が同じかどうかをチェックする。
(define x (list 'a 'b)) (define z1 (cons x x)) (define z2 (cons (list 'a 'b) (list 'a 'b)))
とした場合、z1、z2とも同じ内容のpairではあるが、
racket@> (disp z1) ((a b) a b) racket@> (disp z2) ((a b) a b)
eq?で比較すると、z2の場合は参照先が異なるためfalseが返る。
racket@> (eq? (car z1) (cdr z1)) #t racket@> (eq? (car z2) (cdr z2)) #f
それに対して、equal?は参照先の内容を比較する。
racket@> (equal? (car z1) (cdr z1)) #t racket@> (equal? (car z2) (cdr z2)) #t
JavaScriptの===と==の違いによく似ている。
問題 3.15
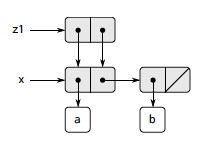
これに対して (set-wow! z1) すると、
シンボル 'a へのポインタが 'wow に書き換わる。
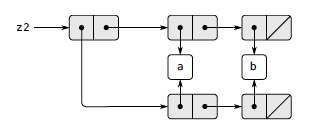
これに対して (set-wow! z2) すると、
(caar z2) のシンボル 'a へのポインタだけが
'wow に書き換わる。
問題 3.16
(define (count-pairs x) (if (not (pair? x)) 0 (+ (count-pairs (car x)) (count-pairs (cdr x)) 1)))
という手続きに対し、使用するpairの数は3ではあるが、 3、4、7、何も返さないようなpairの組み合わせを求めよ。
3は楽勝。
(define 3-pairs (cons 'a (cons 'b (cons 'c nil)))) racket@> (count-pairs 3-pairs) 3
何も返さないリストは循環リストを作ればよい。
(define infinity-pairs (make-cycle (cons 'a (cons 'b (cons 'c nil))))) racket@> (count-pairs infinity-pairs) => 返ってこない...
4と7を返すリストは最初はわからなかったけど、 ノートでポインタ図を弄ってたらひらめいた。
(define p (cons 'b nil)) (define 4-pairs (cons 'a (cons p p))) (define q (cons 'a nil)) (define r (cons q q)) (define 7-pairs (cons r r)) racket@> (count-pairs 4-pairs) 4 racket@> (count-pairs 7-pairs) 7
問題 3.17
問題 3.16 のいずれのリストでも正しく3を返すようなcount-pairsを考えよ。
チェック済みのペアの参照するパンくずリストを用意して、 チェック済みでないペアを見つけた場合は、カウントするように書き換えればよい。
(define (count-proc x) (cond ((not (pair? x)) 0) ((checked-pair? x) 0) ;; チェック済みならカウントしない (else (+ (count-proc (car x)) (count-proc (cdr x)) 1))))
check-pair?の実装を含めるとこんな感じ。 アイデアはすぐに浮かんだけどデバッグに手間取った…
(define (count-pairs-2 x) (let ((bred-crumbs nil)) ; チェック済みのペアかどうかを調べる ; チェック済みでないペアの場合、その参照をパンくずリストに追加 (define (checked-pair? x) (define (iter crumbs) (if (null? crumbs) (begin (set! bred-crumbs (append bred-crumbs (list x))) false) (if (eq? x (car crumbs)) true (iter (cdr crumbs))))) (iter bred-crumbs)) ; ペアの数え上げ手続き。外部環境に ; パンくずリストをおくために内部手続きとする (define (count-proc x) (cond ((not (pair? x)) 0) ((checked-pair? x) 0) (else (+ (count-proc (car x)) (count-proc (cdr x)) 1)))) (count-proc x)))
テスト。
racket@> (count-pairs 3-pairs) 3 racket@> (count-pairs 4-pairs) 3 racket@> (count-pairs 7-pairs) 3 racket@> (count-pairs infinity-pairs) 3
問題 3.18
問題 3.17 を応用して循環リストのチェック処理を作る。
(define (cycle-list? x) (let ((bred-crumbs nil)) ; チェック済みのペアかどうかを調べる ; チェック済みでないペアの場合、その参照をパンくずリストに追加 (define (checked-pair? x) (define (iter crumbs) (if (null? crumbs) (begin (set! bred-crumbs (append bred-crumbs (list x))) false) (if (eq? x (car crumbs)) true (iter (cdr crumbs))))) (iter bred-crumbs)) ; チェック処理 (define (check-proc x) (cond ((not (pair? x)) false) ((checked-pair? x) true) (else (check-proc (cdr x))))) (check-proc x)))
テスト。
racket@> (cycle-list? 3-pairs) #f racket@> (cycle-list? 4-pairs) #f racket@> (cycle-list? 7-pairs) #f racket@> (cycle-list? infinity-pairs) #t
問題 3.19
問題 3.17、18 のパンくずリスト戦略だと、リストの長さに応じて スペースが大きくなっていくので、「一定量のスペース」では計算できないが…
うーん、思いつかないのでパス。
変更は単なる代入
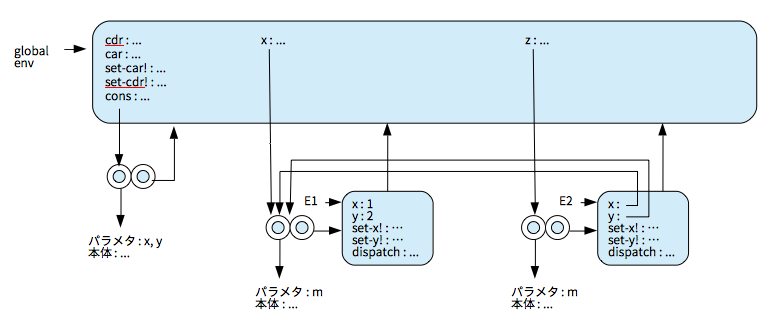
問題 3.20
cons を定義した直後。

(define x (cons 1 2)) を実行後。
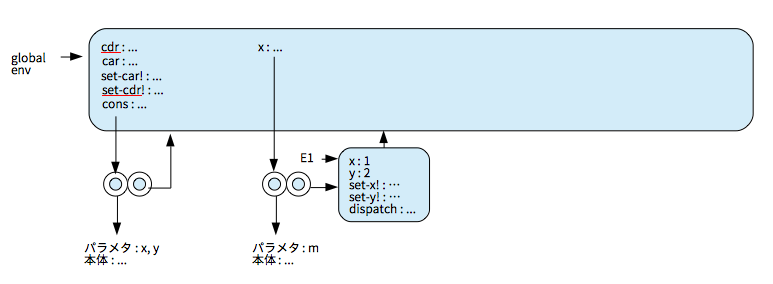
(define z (cons x x)) を実行後。
次は「§3.3.2 キューの表現」から。