SICP 読書ノート#3 - 1.2 手続きとその生成するプロセス(pp.5-30)

作用的順序と正規的順序

正規的順序 (normal-order evaluation) : 値が必要になるため被演算子を評価しない
作用的順序 (applicative-order evalutation) : 関数の引数に演算子と被演算子を含む場合、先に評価する

問題 1.5

Scheme解釈系が正規的順序が作用的順序かをテストする問題

解釈系が正規的順序なら、

(test 0 (p))
-> (if (= 0 0) 0 (p))
-> 0

作用的順序なら、

(test 0 (p))
-> (p) がループで評価され続けて戻ってこない

結果は後者のため、作用的順序。

問題1.6

Alyssaが実装したnew-ifは正しく動作するか？

(define (new-if predicate then-clause else-clause)
  (cond (predicate then-clause)
        (else else-clause)))

(define (sqrt-iter guess x)
  (new-if (good-enough? guess x)
          guess
          (sqrt-iter (improve guess x) x)))

(define (sqrt x)
  (sqrt-iter 1.0 x))

置き換えモデルで考えてみる。

(sqrt 2)
-> (sqrt-iter 1.0 2)
-> (new-if (good-enough? 1.0 2) 1.0 (sqrt-iter (improve 1.0 2) 2))
-> (new-if false 1.0 (sqrt-iter 1.5 2))

applicative-orderのため、この後に (sqrt-iter ...) が評価されるが、さらにその中で (sqrt-iter ...) となり返らなくなる。

Alyssaを助けるなら、new-ifをmacroで実装すればよいのかも？

束縛変数

ここで登場。

手続きの仮パラメタには, 手続き定義の中で, 仮パラメタがどんな名前を持っていても構わないという,特別な役目がある. そういう名前を束縛変数(bound variable)といい, 手続き定義は仮パラメタを束縛する(bind)という. 定義の中で束縛変数名を統一的につけ替えても, 手続き定義の意味は変らない. 変数が束縛されていなければ, 自由である(free)という. 名前が束縛されている式の範囲を有効範囲(scope)という. 手続き定義の中では, その手続きの仮パラメタとして宣言された束縛変数の有効範囲は, その手続きの本体である.

平たく言うと

束縛変数とは、あるスコープの中で任意の名前で対応づけられたオブジェクト
自由(変数)とは、スコープの中では対応づけのないオブジェクト

さらに、

(define (good-enough? guess x)
  (< (abs (- (square guess) x)) 0.001))

上のgood-enough?の定義では, guessとxは束縛変数だが, <, -, abs, squareは自由である. good-enough?の意味はguessやxについては, <, -, abs, squareとは異る名前である限り, どんな名前を選ぼうと変らない. (中略...) 一方, good-enough?の意味は自由変数の名前と無関係ではない. 意味は記号absは数の絶対値を計算する手続きの名前であるという, (この定義の外の)事実に依存している. 定義の中でabsをcosに置き換えたら, good-enough?は別の関数を求めることになる.

定義(スコープ)の中で束縛していればそれは束縛変数だし、定義の外に依存するのであれば、それは定義(スコープ)の中では束縛されないので、自由ということになる。

手続きとその生成するプロセス

p.17の最後の3行がよくわからない

A procedure is a pattern for the local evolution of a computational process. It specifies how each stage of the process is built upon the previous stage. We would like to be able to make statements about the overall, or global, behavior of a process whose local evolution has been specified by a procedure. This is very difficult to do in general, but we can at least try to describe some typical patterns of process evolution.

手続きは計算プロセスの局所的進化(local evolution)のパターンである. それはプロセスの各段階が, 先行する段階の上にどう構成されるかを規定する. その局所的進化を手続きが規定するプロセスの全体としての, 大局的(global)振舞いについて記述出来たらよいと思う. 一般的には困難だが, プロセス進化の典型的パターンに関しては記述してみることが出来る

どう理解したらいいのだろう？問題を手続きに細分化しそれを組み合わせろくらいの意味？

再帰と反復

再帰的手続きは、再帰的プロセス(recursive process)と反復的プロセス(iterative process)の2つがある
状態変数を用いて作り替えることで、関数の処理を最適化できることも
最初はシンプルな実装を目指して、最適化は必要に応じて行っていくべき

例：両替の計算

(define (count-change amount)
  (cc amount 5))

(define (cc amount kinds-of-coins)
  (cond ((= amount 0) 1)
        ((or (< amount 0) (= kinds-of-coins 0)) 0)
        (else (+ (cc amount
                     (- kinds-of-coins 1))
                 (cc (- amount
                        (first-denomination kinds-of-coins))
                     kinds-of-coins)))))

(define (first-denomination kinds-of-coins)
  (cond ((= kinds-of-coins 1) 1)
        ((= kinds-of-coins 2) 5)
        ((= kinds-of-coins 3) 10)
        ((= kinds-of-coins 4) 25)
        ((= kinds-of-coins 5) 50)))

(count-change 100)の評価を木構造プロセスで書きおこしてみる。

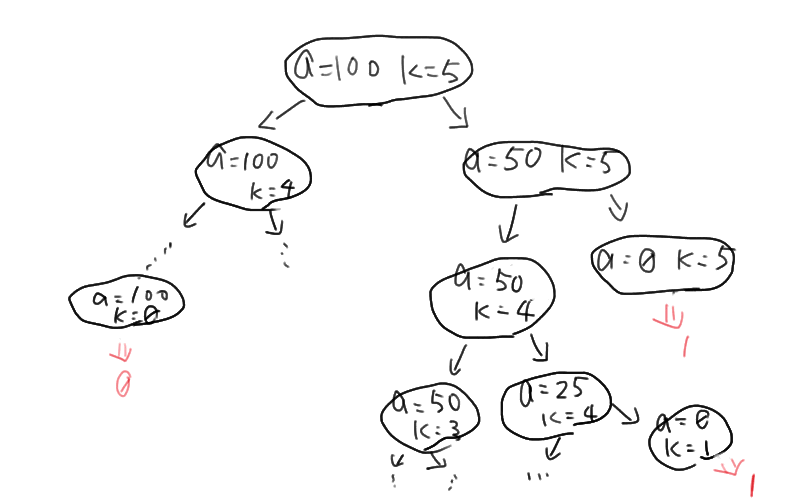
tree structure process

amountがきれいに0になった（=硬貨で割り切れた）枝は両替可能な枝なので、それだけカウントすればよい。

反復的プロセスでも実装し直せそうだけど、どうすればいいだろう？できそうだけど、今の僕の実力だとうまい方法が思いつかない。

問題 1.11

再帰的プロセス。これはすぐにわかる。

(define (f n)
  (if (< n 3)
      n
      (+ (f (- n 1)) (* 2 (f (- n 2))) (* 3 (f (- n 3))))))

反復的プロセス。こっちは手こずった。

;; a <- a + 2b + 3c
;; b <- a
;; c <- b
;; と素直に実装
(define (f n)
  (define (iter a b c count)
    (cond ((= count 0) c)
          ((= count 1) b)
          ((= count 2) a)
          (else (iter (+ a (* 2 b) (* 3 c)) a b (- count 1)))))
  (iter 2 1 0 n))